Las vacas de Narayana

Como cabe deducir de la correspondiente figura de la semana pasada, los números de Narayana, N(n, k), se pueden interpretar como los distintos caminos de celosía que permiten ir de (0, 0) a (2n, 0) en 2n pasos recorriendo solo las diagonales de las celdillas y con k picos (se entiende por picos los vértices superiores). Por lo tanto, N(4, 4) será el número de recorridos entre (0, 0) y (8, 0) en 8 pasos y con 4 picos, y es fácil ver que solo hay un camino posible, el de la figura, por lo que N(4, 4) = 1.

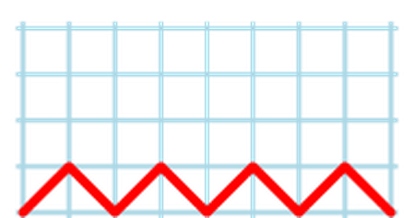
Ya sabíamos, por la mencionada figura de la semana pasada, que N(4, 1) = 1, N(4, 2) = 6 y N(4, 3) = 6, y, como acabamos de ver, N(4, 4) = 1. Por lo tanto, los caminos posibles de la forma N(4, k), son, en total, 1 + 6 + 6 + 1 = 14 (recordemos que k no puede ser mayor que n, por lo tanto, solo puede tomar los valores 1, 2, 3 y 4). Seguro que los comentaristas habituales ven aquí una relación directa con los números de Catalan (¿cuál es?).

Igualmente directa es la relación de los números de Narayana con las palabras de Dyck, de las que nos ocupamos recientemente (¿puedes ver esa relación entre números y palabras?).

Árboles, palabras y números

Hace unas semanas veíamos la relación entre palabras de Dyck y árboles binarios.

En la figura vemos tres árboles enraizados ordenados (que parten de un nodo inicial llamado raíz y se ramifican de arriba abajo) de 4 aristas y 2 hojas (nodos terminales de los que no parte ningún otro). ¿Puedes dibujar alguno más? ¿Cómo se relacionan con los números de Narayana?

Al igual que ocurre con los de Motzkin y los de Delannoy, no hay una fórmula sencilla que dé N(n, k) en función de n y k; hay que utilizar un doble sumatorio, o recurrir a los coeficientes binomiales.

El otro Narayana

Hasta ahora hemos hablado de T. V. Narayana (1930-1987), el matemático canadiense de origen indio que descubrió los números que llevan su nombre. Nombre que comparte con otro ilustre matemático indio: Narayana Pandita (1340-1400), que en su tratado Ganita Kaumudi estudió las que él denominó “sucesiones aditivas”, en las que cada término se obtiene mediante sumas a partir de los términos anteriores, y entre las que se encuentra la famosa sucesión de Fibonacci (y aunque Leonardo de Pisa es un par de siglos anterior, es muy probable que Narayana descubriera la misma sucesión independientemente).

En lugar de conejos, el matemático indio utilizó (mentalmente) vacas, más acordes con su cultura, para ejemplificar una sucesión aditiva, planteando lo que desde entonces se conoce como el problema de las vacas de Narayana, que dice así:

Si las vacas tienen una cría cada año, y cada ternera, después de los tres años que necesita para convertirse en una vaca madura, tiene una cría a principio de cada año, ¿cuántas vacas habrá después de 20 años a partir de una primera ternera?

Invito a mis sagaces lectoras y lectores, no solo a calcular cuántas vacas habrá al cabo de 20 años, sino también a confeccionar una tabla con las vacas de cada generación y a sacar las conclusiones pertinentes.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.

Source: elpais.com