Eugenio Calabi, the mathematician captivated by the great thing about house | Coffee and theorems | Science | EUROtoday

The Italian mathematician Eugenio Calabi died on September 25, 2023 on the age of 100 in Beaumont, Bryn Mawr (USA). This 12 months there had been quite a few tributes all through the world, to rejoice his spectacular legacy and his essential contributions to geometry. It is uncommon that the centenary of an essential mathematician, with greater than 70 years of scientific heritage, and three generations of descendants, is widely known underneath his watchful eye – that is what occurred at one of many conferences, held in Hefei (China) -.

Born in Milan, Italy in May 1923, Calabi moved to the United States along with his household at a younger age. He accomplished his research on the Massachusetts Institute of Technology, funded by a prestigious Putnam scholarship, which was additionally acquired by others comparable to Richard P. Feynman, Nobel Prize in Physics, and John Milnor, Fields Medal. In 1950 he learn his thesis at Princeton University on properties of sure geometric areas often called Kähler manifolds. After working as a professor on the University of Minnesota, in 1964 Calabi joined the University of Pennsylvania. A couple of years later, he obtained the distinguished Thomas A. Scott Professor of Mathematics, which he held till his retirement in 1994, when he grew to become professor emeritus on the similar establishment.

His work has left a deep mark on trendy geometry. His obsession was to provide the naked house a “preferred” form, like somebody who molds a chunk of clay along with his fingers looking for a hidden determine, by no means earlier than imagined. For instance, when putting a rope tied at its ends on a flat floor, what’s the most popular form it could actually take? The reply of many might be a circumference, as a result of it’s “the same everywhere” or, maybe, as a result of it’s “the most perfect figure.” A mathematician might add that this notion has to do with a variational property of mentioned curve: it’s the one which maximizes the entire space it incorporates inside.

A mathematical methodology to search out these most popular curves within the airplane – known as stream of common curvature – is the next: we begin from any curve (that doesn’t intersect itself) and make it “evolve” in such a means that it loses space to fixed velocity and its perimeter decreases as rapidly as attainable. Over time the curve might be convex, and can are likely to a circle of smaller and smaller radius till collapsing at some extent. Moments earlier than this collapse, the popular form of the curve is noticed with the bare eye on a really small scale.

If the preliminary curve have been to chop itself, it might develop a singularity or “spike” all through its evolution and this adjustments the popular form of the curve. By putting oneself within the place of the singularity simply earlier than it’s shaped, one observes, by means of a change in scale, the “self-similar” evolution of a curve that comes from an infinite previous: a curve that doesn’t change its form whereas it evolves with the time. In this case, moreover, the curve strikes by translations, that’s, all its factors transfer at a continuing velocity in a set route. Eugenio Calabi found this answer to imply curvature stream within the Eighties and named it La Parca (the Grim Reaper).

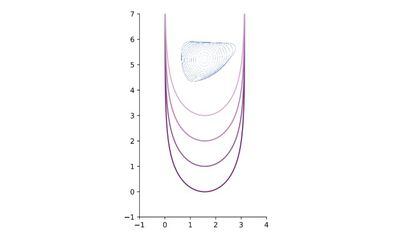
It appears that Calabi made this discovery throughout a tea break, in the midst of a dialog, surrounded by his colleagues. The Grim Reaper seems to be the one answer outlined from an infinite previous time of the stream of imply curvature that evolves by translations: an important property that may solely be understood a few years later. This is presumably one in every of Calabi’s most original traits: his affect on the work of his colleagues typically occurred by means of lengthy casual conversations, with eager observations and key examples, which might later turn into basic items of future mathematical theories. In the phrases of Edoardo Vesentini (researcher on the Scuola Normale Superiore di Pisa): “in the most intimidating theories and in those theorems that tormented me the most, Calabi’s simple explanations arrived.”

In his case, these explanations appeared to return from an instinct or aesthetic style. As Calabi himself defined on a go to to Spain in September 2000: “The main source of geometric intuition is, ultimately, linked to our sensory perceptions of the world. Of course, as we get to more abstract areas, one has to interpret what sensory experience means. I have tried to make this as visible as possible to convey this idea.”

The pleasure of pure discovery and the great thing about geometry have been, actually, two driving forces of Calabi’s arithmetic. However, his work has turned out to have essential implications in different utilized fields, comparable to theoretical physics. As Calabi himself described, mathematicians “invent imaginary worlds, and scientists decide much later whether these can harbor genuine scientific theories.” One of those worlds imagined by Calabi was born from finding out the popular form of an essential class of geometric areas often called complicated manifolds. These objects are made inflexible by offering them with a notion of distance (known as the Kähler metric). The most popular form of this house is given by selecting, amongst all of the attainable metrics, the one which makes the house curve extra homogeneously. A selected case of this downside is named the Calabi downside. For greater than 20 years, nice mathematicians tried to deal with it, arriving at contradictory options. Finally, in 1978, Shing-Tung Yau solved it, giving rise to the areas popularly often called Calabi-Yau varieties. For this essential achievement, the worldwide mathematical group awarded the Chinese mathematician the Fields Medal in 1982. To at the present time, the overall downside initially posed by Calabi stays open and has had an ideal affect on the event of complicated geometry within the twentieth century. and beginnings of the twenty first century. Much of his exercise has centered for years on the research of the geometries often called Kähler-Einstein, of which the Calabi-Yau manifolds are a selected case.

Calabi’s criterion for locating the popular form of house turned out, years later, to have a deep relationship with the sector equations of normal relativity launched by Albert Einstein. In these equations, the distribution of matter and power in house determines its curvature. In the absence of matter, or once we set up a homogeneous distribution of it, house adopts the popular kind imagined by Eugenio Calabi. Surprisingly, removed from being a mere analogy, Calabi-Yau areas, with their lovely geometric shapes, play a key function in some trendy bodily theories that handle the issue of quantum gravity, such because the well-known superstring idea.

Mario Garcia Fernandez He is a Ramón y Cajal researcher on the Autonomous University of Madrid and a member of the Institute of Mathematical Sciences (ICMAT).

Oscar García-Prada He is a analysis professor on the Higher Council for Scientific Research and a member of ICMAT.

Coffee and Theorems is a piece devoted to arithmetic and the atmosphere through which it’s created, coordinated by the Institute of Mathematical Sciences (ICMAT), through which researchers and members of the middle describe the newest advances on this self-discipline, share assembly factors between arithmetic and different social and cultural expressions and keep in mind those that marked their growth and knew rework espresso into theorems. The title evokes the definition of the Hungarian mathematician Alfred Rényi: “A mathematician is a machine that transforms coffee into theorems.”

Editing and coordination: Agate A. Rudder G Longoria (ICMAT).

You can observe MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly e-newsletter.