Mathematics: 2024 and tetrahedral numbers | The sport of science | EUROtoday

I’ve to begin by correcting an omission: final week I talked about 2024 and sq. pyramidal numbers, and I didn’t point out that 2024 can also be a pyramidal quantity, though not sq. however triangular. Fortunately, my sort readers are normally on level: Javier Tamames jogged my memory that 2024 is a tetrahedral quantity (as triangular pyramidal numbers are additionally known as) and Ignacio Larrosa despatched an eloquent visualization within the form of a triangular pyramid of stacked spheres, whose 22 ranges add as much as 2024.

A pyramid whose base is a triangle is a tetrahedron, and due to this fact triangular pyramidal numbers are additionally known as tetrahedral. If within the visualization of the stacking of spheres we add these of every stage, ranging from the highest, we acquire the sequence of the tetrahedral numbers (similar to the variety of spheres of the tetrahedra of 1, 2, 3, 4… spheres on either side): 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364…

The successive ranges of the pyramid kind, in flip, the sequence of triangular numbers (displayable as equilateral triangles of spheres):

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78…

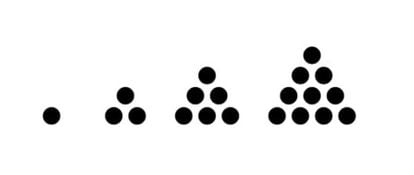
And, due to this fact, the nth tetrahedral quantity (Tn) is the sum of the primary n triangular numbers:

T1 = 1

T2 = 1 + 3 = 4

T3 = 1 + 3 + 6 = 10

T4 = 1 + 3 + 6 + 10 = 20

T5 = 1 + 3 + 6 + 10 + 15 = 35

…

T22 = 1 +3 + 6 + 10 + 15 + 21 + 28… + 210 + 231 + 243 = 2024

Can you discover a method that permits you to decide that the twenty-second tetrahedral quantity is 2024 with out having to carry out the earlier lengthy addition?

Slightly tougher: Comparing the 2 lists above, we see a match: 10, which implies that the third tetrahedral quantity is the same as the fourth triangular quantity. Can you discover extra numbers which are each triangular and tetrahedral?

Even tougher: among the many first tetrahedral numbers there are two which are good squares: 1 and 4. Can you discover any extra or show that they don’t exist?

Zener’s letters

In addition to being a trainer of scientific popularizers, Martin Gardner was a relentless unmasker of fallacies, pseudosciences and numerous paranormalities, and generally mockingly used the arguments of magufos, or their devices, as uncooked materials for his mathematical hobbies.

In an attention-grabbing article introduced up by Manuel Amorós, Gardner begins from Zener’s letters (at this time fallen into well-deserved oblivion, however as soon as very talked-about), used to judge supposed telepathic skills, to pose an attention-grabbing downside of protecting, which has raised a full of life debate among the many readers (see feedback from final week).

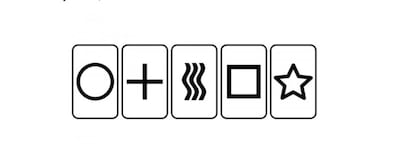
Which of those 5 symbols will be drawn aleph 1 occasions on paper, assuming that they’re drawn with very best traces, with out thickness, and that they don’t overlap or intersect one another? The symbols will be of various sizes, however they should be geometrically comparable. Let us do not forget that alef 1 is the non-countable infinity of actual numbers.

It seems that each one however one of many symbols will be drawn aleph 1 occasions. Can you inform which one it’s and why? A double query with two ranges of problem, as a result of it’s comparatively straightforward to exhibit that the 4 drawable symbols numerous (actually) occasions are, thus figuring out, by elimination, the one that isn’t. But demonstrating why it isn’t so is now not so easy, and Gardner himself limits himself to outlining an answer that isn’t solely clear.

You can observe MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly publication.