The tower and the hypercube | The recreation of science | EUROtoday

In a trivial tower of Hanoi with two discs, A and B, as we noticed final week, the sequence of actions to hold out the switch from one axis to a different is ABA. In the three-disc one, A, B and C, the sequence is ABACABA. That is, first we transfer the three higher discs as within the three-disc tower, then we alter the axis of the fourth disc, and eventually we repeat the switch of three discs to put them on the fourth. And with 4 discs, A, B, C and D, the method is analogous: we transfer the primary three to a different axis, we alter the fourth to the free axis and we repeat the sequence of the primary three to put them on the fourth: ABACABADABACABA. Therefore, because the variety of disks will increase, the variety of strikes required will increase in response to the sequence 1, 3, 7, 15, 31, 63… For n disks, the variety of strikes required is 2ⁿ– 1, which is explains the numerical coincidence between the 2 supposed Indian legends: that of the inventor of chess and that of the tower of 64 gold discs within the temple of Benares.

As we additionally noticed, the sequence of actions essential to maneuver a tower of three disks corresponds to the Hamiltonian path by the vertices of a dice. But the factor doesn’t finish there (it has solely simply begun): the sequence of actions for a tower of 4 disks corresponds to the Hamiltonian route by the vertices of a tesseract (four-dimensional hypercube). And so on and so forth indefinitely: because the mathematician DW Crowe demonstrated within the mid-Twentieth century, this correspondence holds for towers of any peak and cubes of any dimensions: the variety of actions and the order through which n disks have to be moved from one tower of Hanoi to switch them to a different axis, correspond precisely to the directional (and dimensional) sequence of a Hamiltonian path in an n-dimensional hypercube.

Two picket puzzles designed across the similar time by two nice mathematicians, Hamilton's dodecahedron and Lucas's Tower of Hanoi, coincide on a shelf in a toy retailer. At first look plainly they don’t have anything to do with one another; however, as in nineteenth-century cleaning soap operas, they find yourself discovering that they’re (topologically) brothers.

Calligraphic graphs

For the primary time in 9 years, final week, as a consequence of a technical challenge, the feedback part was not operational, so I'll return to 2 weeks in the past. Bretos Bursó despatched, in define, his resolution to the Hamiltonian tour by the vertices of a dodecahedron:

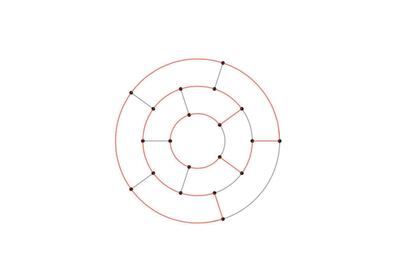
And Salva Fuster made an fascinating commentary in regards to the relationship between graphs and letters: “Thinking about Eulerian and Hamiltonian paths, I have realized that neither E nor H admit paths of one type or the other. I suppose that the simplest graph that does not support them coincides with the letter Y. By the way, the letters of the alphabet could be classified into different types of graphs. “How many types are there?”

I encourage my astute readers to look at the letters (uppercase) of the alphabet thought of as graphs. The Ñ is omitted for apparent causes (it can’t be thought of a graph because of the tilde) and it is strongly recommended to give attention to a typeface with a easy stroke (dry stick or sans serif, as typographers say), like this:

A B C D E F G H I J Ok L M N O P Q R S T U V W X Y Z

You can observe MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly publication.