Sacred polygons and cursed stars | The recreation of science | EUROtoday

As we noticed final week, the facilities of the circles of radii 1, 2 and three tangent to one another are the vertices of a proper triangle. And not simply anybody, however the one with sides 3, 4 and 5, none apart from the sacred triangle of the Egyptians, who knew that the angle reverse the longest aspect of this triangle was proper, though it’s not sure that they generalized this end result to all of the triangles whose sides fulfill the connection a² = b² + c² (that’s, they knew the Pythagorean theorem).

As Salva Fuster factors out: “For the circles tangent to each other with radii 1, 2 and 3, once their centers have been drawn forming a right triangle with sides 3, 4 and 5, it is easy to see that the radius of the outer tangent circle to those three It will be 6, and that its center will be found precisely at the point that would form a rectangle with the other three centers.” (Because?).

Finding the radius of the inside tangent circle by geometric strategies will not be so easy. We can resort to the system:

Q² + R² + S² + T² = 1/2 (Q + R+ S + T)²

But, as we noticed, the calculations are lengthy and cumbersome, so it’s handy to make use of one other system that provides us T instantly:

T = Q + R + S + 2√(QR + QS + RS)

T = 1 + 1/2 + 1/3 + 2√(1/2 + 1/3 + 1/6) = 11/6 + 2 = 23/6

Therefore, the radius of the internal tangent circle might be 1/T = 6/23

If we apply the unfavorable worth of the basis:

T = 11/6 – 2 = –1/6

Which corresponds to the radius of the outer tangent circle, which as we’ve seen measures 6 items, contemplating its curvature unfavorable (within the case of the internal tangent circle the 4 circles “kiss” with their convex elements, whereas the outer tangent circle kisses the one other three with their concave half).

From the sacred triangle to the diabolical pentacle

The golden triangle of the Egyptians will not be the one sacred, golden, mystical… or cursed polygon. Without leaving the scope of triangles, the equilateral triangle can be the sacred triangle par excellence, because it represents God himself (the Holy Trinity), and never just for Christianity: for Hinduism it’s also the logo of the divine triad: Brahma, Vishnu and Shiva.

Among the quadrilaterals, the golden rectangle stands out, whose sides are within the -divine- proportion 1:1.618 (do you keep in mind why or are you able to deduce it?). The acquainted DIN A4 folio, measuring 210 x 297 mm, will not be fairly gold, nevertheless it has an attention-grabbing geometric property that makes it very particular (which one is it?). Another ubiquitous rectangle is the domino or tatami, with sides within the proportion 1:2, which we steadily discover in bricks and tiles, as a result of benefit of with the ability to couple two smaller sides with a bigger one to construct partitions or tile flooring.

In the case of the common pentagon, it’s its diagonals that decide the sacred determine: the pentacle, pentagram or pentalpha, the five-pointed star honored by the Pythagoreans. Among different geometric subtleties, the aforementioned divine proportion nests within the pentagonal star. (Can you discover it?)

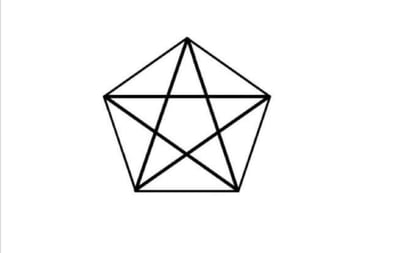
If we draw the diagonals of the internal pentagon of the pentacle, we receive one other one, however inverted, an inversion that isn’t solely spatial, because the pentacle the wrong way up is a diabolical image, whose curse will attain you if you don’t decide the proportion between the world of ​​the pentacle and the of its inside antipentacle. Or in case you don't draw them correctly, for which it’s important to begin by drawing a daily pentagon with a ruler (not graduated) and a compass.

In the case of the common hexagon, the development may be very easy, because the aspect of the hexagon is the same as the radius of the circumscribed circle, and it’s simply as straightforward to assemble an equilateral triangle or a sq.; however within the case of the pentagon it should value you a bit of extra. If you succeed, attempt different common polygons: octagon, enneagon, decagon… till you attain the elusive heptadecagon (17-sided polygon). Cheer up, Gauss bought it when he was solely 19 years previous.

You can comply with MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly e-newsletter.