Borges and the infinite | The sport of science | EUROtoday

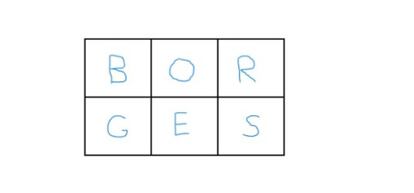
It is just not attainable to reconstruct BORGES from his Nabokovian anagram OSBERG by folding final week's 2×3 map. It is sufficient to understand that the E and the S, which within the phrase BORGES are collectively, within the OSBERG grid occupy squares that solely share one vertex, and no folding could make two squares “opposite by the vertex” adjoining. Consequently, one can’t go from BORGES to OSBERG both: on this case there are two pairs of letters in packing containers reverse the vertex (BE and OS) that in OSBERG go collectively.

Regarding the totally different prospects of folding triptychs, polyptychs and elementary maps, our common commentator Francisco Montesinos has carried out a really detailed evaluation (see feedback from final week) that, for causes of house, I can’t reproduce in full; This is what he says concerning the 2×2 elemental map (and by the way, in parentheses, he alludes to the impossibility that we now have simply seen):

“In the 2×2 case, numbering the sheets (1, 4, 2, 3) from left to right and from top to bottom, there are 24 permutations, of which 8 give impossible configurations (two pages in a diagonal position will have some interleaving) and Of the remaining 16, 8 will be symmetrical, so there will be 8 different possible folds. Another way to reach the same result is considering that if the first sheet is fixed in front view (4 possibilities), for the next one there are only 2 possibilities and only one for the remaining two positions, 8 in total.

Borges dismantled

After the publication of the previous entry of The game of science, Borges deconstruidoan article titled Borges dismantled, and it is hard to believe that, just a few hours apart, two texts with such similar titles are published by pure chance. (I invite my astute readers to calculate “the Fermi way” the order of magnitude of the chance of one thing like this occurring randomly).

In any case, the aforementioned article says, amongst different issues: “At the center of his work, Borges places the idea of ​​infinity, a concept that plays a crucial role in both his narratives and his essays. The infinity of books in The Library of Babelthe mirrors that reflect eternally in Tlön, Uqbar, Third Worldand endless labyrinths are just a few examples of how Borges challenges our understanding of time and space, leading us to question reality itself.”

In (the) actuality (itself), not one of the three issues talked about is infinite: the variety of attainable books is – though immense – finite and even simply calculable, because the German mathematician and thinker Kurd Lasstwiz (1848-1910) already confirmed in his pioneering story The common librarywherein Borges was impressed to jot down The Library of Babel. And the mirrors that mirror one another accomplish that so slowly – on the meager, from an astronomical viewpoint, velocity of sunshine – that the variety of photos they may generate earlier than the universe goes extinct not solely doesn’t It is infinite, however not even very giant in comparison with different numerical monsters (like that of attainable chess video games, for instance).

As for “endless mazes”, can such a factor exist? What would a labyrinth be like, just like the legendary one in Crete, from which it was not possible to get out? Borges, aside from error or omission, doesn’t at any time converse of limitless labyrinths, however he does converse of sure labyrinths from which he exits by at all times turning to the left. What would such a left-handed labyrinth appear like?

The peculiar – and considerably complicated – relationship of the Argentine author with the infinite should be sought, above all, in his tales. The Aleph, The Garden of Forking Paths y The round ruins, and perhaps in some poems. Not in useless El Aleph It is called after “the terrible dynasty” of Cantor's transfinite numbers… But that’s one other article.

You can comply with MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly publication.

_