Machine studying helps assault traditional mathematical issues | Coffee and theorems | Science | EUROtoday

The Hadwiger-Nelson drawback is probably among the finest identified within the space of ​​discrete geometry. It is in regards to the following query: what’s the minimal variety of colours which can be wanted to color the airplane, in such a approach that at all times, when taking any two factors, with a distance of 1 unit between them, they’ve at all times been painted with colours totally different? Even although it’s a seemingly harmless query, it has gone unanswered for greater than 70 years. However, due to machine studying instruments, latest progress has been made in understanding it.

So far, it’s identified that the variety of colours wanted may be 5, six or seven. To examine the minimal variety of colours mandatory, it is sufficient to discover particular configurations of factors on the airplane that can not be painted with a quantity – let’s name them n – of colours and meet the indicated property. Thus, we all know that we want extra, a minimum of, n+1 colours to color your complete airplane – which incorporates that particular drawing – if we wish the property to be verified.

First of all, it’s simple to see that a minimum of three colours are wanted. Indeed, taking an association so simple as the three vertices of an equilateral triangle whose facet measures one, we already want three colours to paint them, in order that there are not any two adjoining vertices with the identical shade – in any other case, these factors wouldn’t fulfill the specified property. : they might be at distance 1 and would have the identical shade.

Refining this sort of argument, within the early 60s of the final century, the brothers Leo and William Moser discovered a concrete configuration of solely seven factors of the airplane that wants a minimum of 4 colours to satisfy the property we wish, which exhibits that the minimal quantity is 4. More lately, in 2018, beginner mathematician Aubrey de Gray discovered a configuration with greater than 1,000 factors on the airplane during which it was mandatory to make use of a minimum of 5 colours for the specified situation to be met.

Furthermore, it’s identified that the variety of colours can’t be greater than seven, as a result of we all know methods to paint the airplane with these colours that obtain our goal. For instance, simply take a honeycomb tessellation and paint one hexagon one shade and the six adjoining ones totally different colours. As the diameter of every hexagon is lower than ½, any two factors at a distance, one at all times fall in several, adjoining hexagons, subsequently, painted in a distinct shade.

But this doesn’t resolve the thriller, there could possibly be one other coloration, that we have no idea but, that requires fewer colours and nonetheless fulfills the property. So, the reply could possibly be 5, six or seven and, for the time being, nobody is aware of the best way to resolve this enigma.

To additional advance analysis, a standard technique in arithmetic is to impose weaker constraints and resolve the ensuing drawback. This typically permits us to search out approaches to resolve the unique query. In our case, to check the weak Hadwiger Nelson drawback, we analyze what occurs if we permit a number of the factors painted with the identical shade to be at a distance totally different from one. To do that, we introduce the notion of a sound configuration of a coloring of the airplane of n colours, with distances (d1, d2, … dn) related to every shade.

For instance, if n=4, the colours are blue, inexperienced, yellow and orange, and the distances 1.5 –related to the colour blue–, 0.2 –with the inexperienced–, 1 –with the yellow–, 3.7 – to orange–, a sound configuration with these values ​​is a set of factors during which each pair of factors coloured with the identical shade is at a distance better than the gap related to that shade. In the instance, there can’t be two blue factors lower than 1.5 aside or two inexperienced factors lower than 0.2.

Thus, discovering a sound configuration of six colours with related distances (1,1,1,1,1,1) would imply displaying that the reply to the Hadwiger-Nelson drawback is, at most, six. Finding a configuration of 5 colours and with distances (1,1,1,1,1) could be even higher, as it will utterly resolve the issue. And, even when they’re much less formidable, discovering configurations of this kind permits us to extend our information in regards to the normal drawback.

Recently, a staff of researchers from the Zuse Institute Berlin (ZIB) and the Technische Universität Berlin (TU Berlin) have made progress on this path. Konrad Mundinger, Sebastian Pokutta, Christoph Spiegel and Max Zimmer have discovered a sound configuration of six colours (1,1,1,1,1,d), the place the worth of d It is between 0.354 and 0.657. In different phrases, the factors coloured with the primary 5 colours keep the situation with a unit distance, whereas for the sixth shade the situation is relaxed: there generally is a pair of factors painted with this shade at a smaller distance, between 0.354 and 0.657. This end result improves earlier outcomes from 1996, increasing the margin of attainable selection for d.

But, additionally, what is basically fascinating is the function that machine studying has performed in acquiring this end result. His thought, broadly talking, has been to coach a neural community to search out representations that meet the specified circumstances, attempting to make the worth of d was as a lot as attainable. This kind of neural networks usually are not able to fixing the issue precisely, however as an alternative receive proposals for approximate options, testing an unlimited variety of attainable combos, which is a process that’s unachievable for people.

The neural community then works as an “approximate oracle”, and it’s the researchers’ job to interpret the data generated and form this path of exploration right into a attainable resolution. With these methods the authors have been in a position to receive varied constructions that enhance all these identified to this point. For instance, they’ve constructed a periodic tessellation (within the picture) that makes use of six colours, during which the sixth shade, purple, is the one which meets essentially the most lax circumstances.

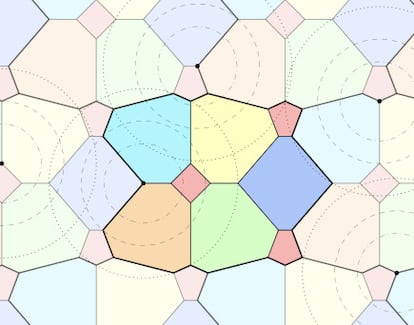
This kind of computational methods are very promising and it’s attainable that sooner or later they are going to make it attainable to cope with different issues that right now are unapproachable, comparable to, for instance, the examine of the identical drawback in area – as an alternative of within the airplane -, or the issue of Hadwiger-Nelson in its entirety.

Juanjo Rué He is an adjunct professor of the Department of Mathematics of the Polytechnic University of Catalonia (UPC), member of the UPC Mathematics Institute (IMTech) and researcher assigned to Mathematical Research Center (CRM).

Agata A. Timón G Longoriacoordinator of the ICMAT Mathematical Culture Unit.

Coffee and Theorems is a bit devoted to arithmetic and the atmosphere during which it’s created, coordinated by the Institute of Mathematical Sciences (ICMAT), during which researchers and members of the middle describe the most recent advances on this self-discipline, share assembly factors between arithmetic and different social and cultural expressions and keep in mind those that marked their growth and knew the best way to remodel espresso into theorems. The title evokes the definition of the Hungarian mathematician Alfred Rényi: “A mathematician is a machine that transforms coffee into theorems.”

Editing, translation and coordination: Agate Timón García-Longoria. She is coordinator of the Mathematical Culture Unit of the Institute of Mathematical Sciences (ICMAT)