A probabilistic monster | The science sport | EUROtoday
Regarding the issue of the beads of the concentric necklaces, which had been left pending, that is the remark of Manuel Amorós:
“I think only odd numbers can be a solution. To see this we can take natural numbers instead of colors. The necessary condition is that each number is separated from its homonym by a quantity, and these quantities must be different. Therefore, we should have an expression of the type:
1 + 0 = 1
2 + a = b
…
n + t = p
It cannot appear in the second column nwith which and taking into account that the second column runs through 0.1… n-1 and the third runs through 1, 2… nwe can add obtaining (n+1, 2) + (n, 2) congruent (n+1, 2) (modulo n). Then the necessary condition is that (n, 2) is a multiple of n. That can only happen if n is odd.
On the other hand, it is a sufficient condition. We can place the homonymous numbers one unit less away than said number. For example, for n =5:
1 + 0 = 1
2 + 1 = 3
3 + 2 = 5
4 + 3 = 2
5 + 4 = 4″.
But the problem has raised other interesting reflections (cf. comments on The Juice of the Minority), and is one that lends itself to further investigation.
Schrödinger’s symbiote
On the other hand, a comment by Salva Fuster gives rise to the “meta-problem” of the symbiote:
“The symbiote problem sounds familiar to me, having been dealt with quite a long time ago. If I remember correctly, one question that was raised was the conservation of mass. Subdivisions might not be possible if the division capacity of matter had a lower limit.”
It sounds acquainted to me too, however for the reason that challenge of the stochastic monster just isn’t within the title, I can not find it (somebody could also be stunned that I do not management all of the installments of The Science Game, however that is the quantity 495). No doubt a diligent reader will discover the article in query and we are able to return to the subject. Or, higher but, we are able to seek the advice of the Introduction to chance principleby William Feller, as Francisco Montesinos suggests:
“To know if the process ends in a population N = 0 or develops without limit, we must rather look at whether E (expected number of direct descendants) is <= 1, in which case it ends up dying, or E > 1 in which case it develops without limit. In the given case, since E > 1 it will never die. See Feller, p. 301 et seq.
This opinion contrasts with that of other readers, who believe that the symbiote will surely die. What are we left with? Will he be Schrödinger’s monster, alive and dead at the same time until we open the vault in which he is locked?
Paradoxical networks
Regarding the Braess paradoxFuster comments:
“Another case of Braess’s paradox could occur in packet-switched networks, in which enabling new routes between network nodes could cause longer message sending times, although I think it is a case very similar to that of roads.” To which one other reader provides: “In truth, basically the paradox is noticed within the movement in networks. In 1990, British Telecom suffered an actual disaster within the habits of the community.
And once again my kind readers have filled the section. I only have to raise a problem related to one of the topics discussed recently. Like the following, proposed at the time by Josep María Albaigès in his excellent magazine Carrollia:
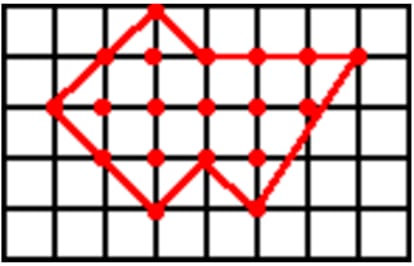
Suppose a floor of sq. tiles measuring one meter on either side, on it we draw a polygon as whimsical as we like (see the determine) fashioned by straight strains that completely be a part of vertices of the tiles. we are going to name N to the variety of vertices which can be on the perimeter line and B to the variety of vertices contained in the polygon. It is about discovering a formulation that, relying on N y Bpresent the worth of the realm of the polygon.
https://elpais.com/ciencia/el-juego-de-la-ciencia/2024-11-29/un-monstruo-probabilistico.html
