Fierce pigeons | THE GAME OF SCIENCE | EUROtoday

We picked up final week what number of smaller equilateral triangles are at the least must cowl an equilateral triangle. These smaller triangles shouldn’t have to be the identical and might overlap. The reply is 3, and it’s reached by the exclusion of the minor risk: it’s evident that with 3 it’s doable, and it’s not troublesome to show (how?) That with 2 it’s not.

As for the issue of the 5 factors of an equilateral triangle, alternative ways of addressing it have been proposed; The most “palomera”, that of Francisco Montesinos:

“Uniting the midpoints on the sides of the original equilateral triangle, 4 equilateral triangles of side 1/2 m are obtained. There will necessarily be 2 points of the 5 dice within the same triangle of the latter reduced, then their distance d may not be D> 1/2”.

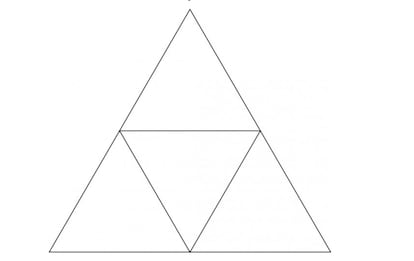
Indeed, by dividing the preliminary triangle into 4 equal triangles, a 4 containers are created wherein 5 pigeons are to be accommodated, that’s, factors. And the very best distance that may be in an equilateral triangle 1/2 m is exactly the size of the aspect, so 2 factors situated in it will probably, at most, be 1/2 m away (and are, clearly, the vertices of the triangle).

The resolution supplied by Rafael Granero is considerably extra difficult, however not much less fascinating:

“Certainly, there are 4 factors that comply which are additional away, and it will probably even be stated that, given 4 factors, they’re the furthest who could also be amongst them: the three vertices and the middle. The heart is 57.7 cm from any of the three vertices. Any motion, nonetheless small, from the purpose situated within the heart will íludibly make that the space to 1 or two of the vertices decreases. situated within the vertices with respect to the opposite three factors.

As in passing, the query of how unlikely it’s that it’s a must to launch a cube 13 occasions to acquire 3 equal numbers, and that is the reply of Juan Zubieta:

“The probability of reaching the 13 is the quotient between the possible permutations with 6 couples of numbers (12!/2^6) and all the sequences of possible rolls (6^12). The result comes out: 1925/559872 (approximately one possibility between 291).” (Remember that it’s not about acquiring a particular quantity 3 occasions, for instance on 6, however that some quantity comes out at the least 3 occasions).

High -risk

After the coaching of the final weeks, and particularly devoted to those that assume that the precept of the palomar is a perogrullada solely relevant to the only issues, here’s a traditional that deserved the eye of Paul Erdös himself:

Given the set {1, 2,…, 2N}, show that in any subset of n+1 numbers there can be at the least two such that one is a a number of of the opposite.

Do not attempt to resolve it within the most warmth hours: the pigeons of this excessive -risk dove may fry the neurons.