The artwork of folding maps | The sport of science | EUROtoday

If we multiply the edges of the DIN A0 sheet, the origin of the DIN sequence, one by the opposite, as we noticed final week, we get hold of:
841 mm x 1189 mm = 1000049 mm²
that’s, virtually precisely one sq. meter, as Erwin Schorr factors out in his remark, with an error of simply 5 hundred thousandths.
Regarding the opportunity of reaching the Moon by folding paper, here’s what Salva Fuster feedback:
“With the thickness of the paper being approximately one tenth of a mm, by folding it 10 times we will have 210 times the initial thickness, which means having approximately 1,000 times more than the initial thickness, that is, 100 mm (0.1 m) thick. . Now, every time we fold 10 more times, the thickness will be multiplied by 1,000. Therefore, if we make 40 folds from the initial situation, we will have: 0.1 mm – 100 mm – 100 m – 100 km – 100,000 km With a couple of additional folds we would already exceed the distance to the Moon, since by making two more folds we would multiply the last of the previous values by 4. In conclusion, 42 folds is enough. Regarding the size of the sheet, taking into account that an A4 sheet of paper can be folded up to 7 times, A3 could be folded 8 times, A2 9, A1 10 and A0 11 times, that is, a sheet of 1 m². It could be folded 11 times. If we want to reach 42 folds, we will have to double it 31 times more, which would mean increasing the surface area to 2³¹ m², that is, about two billion square meters, or in other words, about 2,000 km², a size similar to the from Gipuzkoa. Now, it would surely be better to use a strip of paper and not a sheet of paper proportional to a DIN A4″.
As for the reason for the areas of the pentacle and its inner antipentacle, if you have not found it with the clues given last week you deserve to fall into the clutches of the Evil One, since the thing is as easy as realizing that the side of the pentagon regular whose diagonals form the pentacle is 1 + Φ = 2.62 times greater than the side of the inner pentagon, whose diagonals form the antipentacle; Therefore, the area of the pentacle will be 2.62² = 6.86 times greater than that of the antipentacle.
Irritating road maps
Younger people may never have had to deal with a road map, now that every cell phone and every car has access to GPS; But those of us who come from the last century have seen on more than one occasion how easy it is to unfold a map and how difficult it is to fold it again properly.
Let us consider a trivial case: a map with a single vertical fold, V1, like the one in the figure. We can only fold it in two ways: hiding the front, A, or hiding the back, R, and we can designate these folds as V1A and V1R.
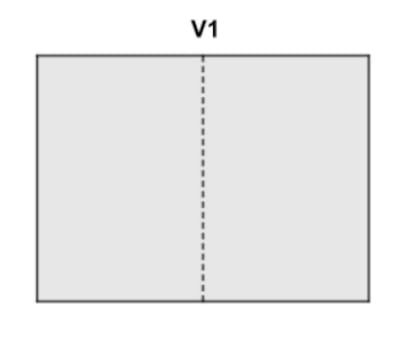
If instead of being divided into two halves, the elemental map were divided into three parts by two vertical folds (as is in fact normal in some pamphlets, not in vain called triptychs), in how many different ways could we fold it?
V1A-V2A, V1A-V2R, V1R-V2A…
Spoiler: they may seem like 8 (4 starting with V1 and 4 starting with V2), but there are actually 6 (why?). And it could also seem that 6 is the result of 3! = 3 x 2 x 1, and that, therefore, in the case of three vertical folds we would have 4! = 24 different bends, but it's not like that. How many different ways can a “quatriptych” be folded?
The basic drawback, with n folds, which appears comparatively easy, is advanced and elusive, and is additional sophisticated if, as within the case of actual maps, there are each vertical and horizontal folds; In reality, no clear components or algorithm has but been discovered to handle the “irritating” (as mathematicians themselves have referred to as it) drawback of map folding.
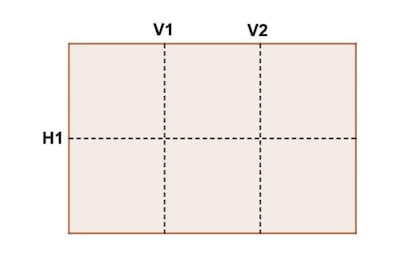
If you wish to see for your self how irritating it’s, attempt to decide what number of alternative ways you possibly can fold the easy map within the determine, with two vertical folds and only one horizontal fold.
You can observe MATERIA in Facebook, X e Instagramclick on right here to obtain our weekly e-newsletter.
https://elpais.com/ciencia/el-juego-de-la-ciencia/2024-05-03/el-arte-de-doblar-mapas.html
